Die Welt des Optionshandels ist voller kurioser Bezeichnungen. Zu diesen Begriffen zählen zweifellos die “Optionsgriechen”. Dabei handelt es sich um hilfreiche Berechnungen für den Handel mit Optionen, für die Optionstrader diese griechischen Symbole verwenden. Wie diese Kennzahlen im Optionshandel genau funktionieren und wie man sie zum Vorteil nutzen kann, erfahrt ihr in diesem Blogbeitrag über die Optionsgriechen.
Das Wichtigste in Kürze
- Die Optionsgriechen geben Auskunft, um wie viel sich ein Optionspreis bewegt, wenn sich ein bestimmter Einflussfaktor (Preis, Volatilität, Zeit) verändert
- Das Delta gibt die Änderungsrate des Optionspreises an, falls sich das Underlying um $ 1 ändert
- Das Gamma gibt die Änderungsrate des Deltas an, falls sich das Underlying um $ 1 ändert
- Das Theta gibt die Änderungsrate des Optionspreises pro Tag an
- Das Vega gibt Änderungsrate des Optionspreises in Abhängigkeit der Volatilität an
Einfluss der Options-Griechen auf den Optionspreis
Optionen verhalten sich in der Regel nicht wie ihr Basiswert (Underlying). Steigt der Kurs unseres Basiswerts etwa um 10 %, könnte unsere Option gleichzeitig um 50 % steigen. Denn es fließen weit mehr Faktoren als die reine Kursbewegung des Basiswertes in die Optionspreisbildung mit ein. Die Griechen oder auch Greeks berücksichtigen nicht nur diese reine Kursveränderungen, sondern auch die Veränderungen des Basiswertes, der Restlaufzeit oder auch der Zu- oder Abnahme der impliziten Volatilität.
Diese Optionskennzahlen heißen Griechen, da der Ursprung in der Black-Scholes-Formel für die Berechnung von Optionspreisen liegt. Diese mathematischen Herleitungen werden in der Regel mit griechischen Kennzahlen ausgedrückt. Jeder Optionsgrieche verändert sich während der Laufzeit von Optionen und beeinflusst dadurch den Optionspreis.
Die wichtigsten Sensitivitätskennzahlen sind diese fünf Options-Griechen:
- Delta
- Gamma
- Theta
- Vega
- Rho
Mit den Griechen lässt sich die Veränderung des Optionspreises der verschiedenen Veränderungen von impliziter Volatilität, Zeit oder Bewegungen des Basiswertes sinnvoll abschätzen.
Das Delta einer Option
Bekannt aus dem Mathematikunterricht und dem Alltag ist das Delta. Es bezeichnet stets eine Veränderung – und der Optionshandel ist dabei keine Ausnahme. Hier bezieht sich das Delta einer Option auf die Kursveränderung des Basiswertes. Dabei drückt das Delta aus, was mit dem Optionspreis passiert, wenn sich der Kurs der Underlyings um genau $ 1 verändert.
Das Wichtigste zum Optionsgriechen Delta:
- Einflussgröße auf den Optionspreis, wenn sich der Kurs des Basiswertes um $ 1 ändert
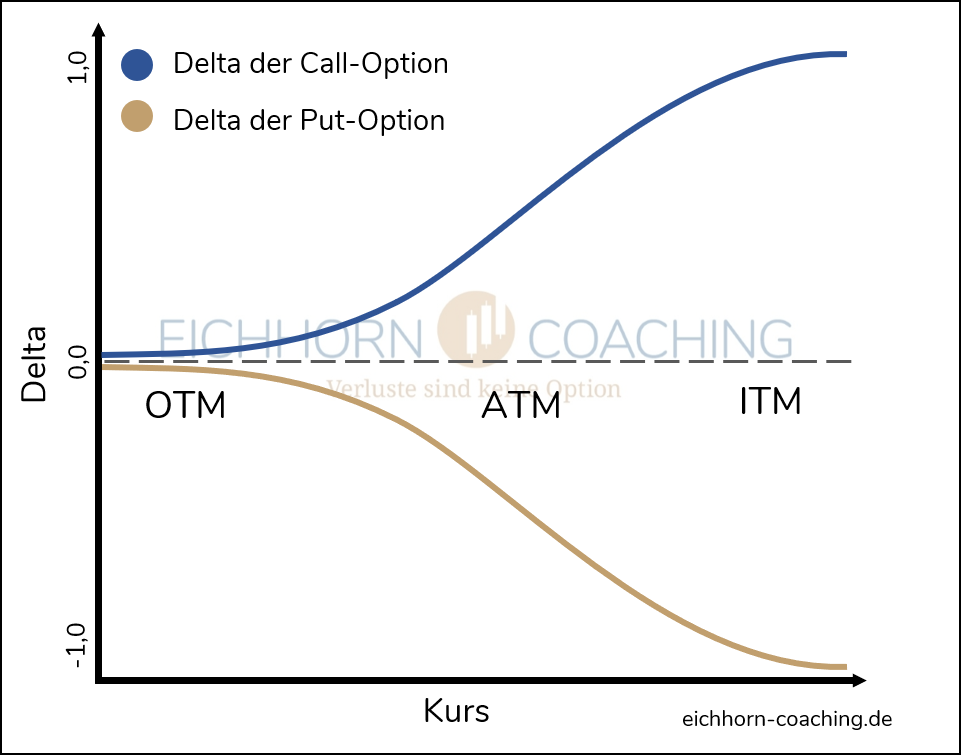
- Dezimalkennzahl, die die Werte zwischen -1 und 1 annehmen kann
- immer positiv bei einer Call-Option
- immer negativ bei einer Put-Option
Da alle Griechen immer vom Kauf einer Option ausgehen, kann unser Delta bei Call-Optionen ausschließlich positiv sein. Denn steigt der Wert des Underlyings um einen Dollar, muss auch der Wert einer Kauf-Option (Call) ansteigen. Bei Put-Optionen ist das Gegenteil der Fall, sodass unser Delta immer nur negativ sein kann.
Mehr zum Delta könnt ihr in diesem Blogbeitrag nachlesen: Das Delta einer Option – Erklärung & Beispiele
Beispiel Delta einer Option
- Kurs der Aktie $ 196
- Preis der Call-Option: $ 1,00
- Delta: 0,10
- Annahme: Aktie steigt um $ 1 auf $ 197
- Veränderung des Optionspreises: $ 1,00 + 0,10 (Delta) = $ 1,10
Eine Aktie im Wert von $ 196 Dollar steigt um einen Dollar. Die Option hat einen Preis von ebenfalls einem Dollar und das Delta der Option liegt bei 0,10. Mit dem Anstieg des Aktienpreises um $ 1 steigt auch unser Optionspreis um das Delta, sodass wir $ 0,10 addieren müssen. Der neue Preis der Option beträgt im Anschluss also $ 1,10.
Das Gamma einer Option
Ein weiterer, wichtiger Optionsgrieche ist das Gamma. Das Gamma einer Option nimmt direkt Bezug auf das Delta und gibt an, wie sich das Delta verändert, wenn der Kurs des Underlyings um $ 1 schwankt. Das Gamma ist dabei stets positiv.
Das Wichtigste zum Optionsgriechen Gamma:
- Gibt die Änderungsrate des Deltas an, falls sich der Basiswert um $ 1 bewegt
- ist immer positiv
- Je näher die Option am Geld ist, desto größer wird das Gamma
- Je kürzer die Restlaufzeit ist, desto größer sind die Schwankungen des Gammas
Mehr zum Gamma könnt ihr in diesem Blogbeitrag nachlesen: Das Gamma einer Option – Erklärung & Beispiele
Kostenloses E-Book für Optionseinsteiger


- Optionsbegriffe im Überblick: Innerer Wert, Moneyness, Griechen und alles zu impliziten Volatilität
- Stillhalterstrategien: Short Put, Bull Put Spread, Short Call und Bear Call Spread
- Investorenstrategien: Cash Secured Put und Covered Call
- Was tun im Verlustfall? Follow-Up Aktionen
- zahlreiche Case Studies
Mit der Anmeldung stimmst du zu, dass du die Datenschutzerklärung und den Risikohinweis gelesen hast. Abmeldung vom Newsletter jederzeit möglich.
Beispiel Gamma einer Option:
- Kurs der Aktie $ 196
- Preis der Call-Option: $ 1,00
- Delta: 0,10
- Gamma: 0,03
- Annahme: Aktie steigt um $ 1 auf $ 197
- Neues Delta der Option: 0,10 (altes Delta) + 0,03 (Gamma) = 0,13
In der Praxis steigt der Gamma-Wert und damit das Delta einer Option immer weiter an, je näher eine Option am Geld (“at the money”) ist (mehr zur Moneyness: Blogbeitrag: Berechnung des inneren Wertes einer Option). Dies kann beim Verkauf einer Option schnell große Probleme bereiten, wenn nur noch eine kurze Restlaufzeit besteht und der Kurs des Underlyings immer weiter gegen einen läuft. Zur Berechnung des Effekts bei kurzlaufenden Optionen wird der Gamma-Wert zu unserem Delta hinzuaddiert. Daher führt das meist schnell ansteigende Gamma zu einem exponentiellen Wachstum des Deltas und damit der Kosten.
Das Vega
Die Änderungsrate unseres Optionspreises hängt auch von der jeweiligen impliziten Volatilität ab und wird mit dem Buchstaben Vega angegeben. Nimmt die Volatilität zu, wird eine Option teurer; nimmt sie ab, sinkt der Preis.
Das Wichtigste zum Options-Griechen Vega:
- Änderungsrate des Optionspreises in Abhängigkeit der Volatilität
- Bei einer Zunahme der Volatilität wird der Optionspreis teurer
- Bei einer Abnahme der Volatilität wird der Optionspreis günstiger
- Je länger die Restlaufzeit ist, desto größer ist das Vega
- Das Vega ist bei ATM-Optionen am größten
Das Vega wird stets in Prozent angegeben und addiert oder subtrahiert diesen Wert von dem Optionspreis – je nachdem, ob die Volatilität steigt oder fällt. Der Preis einer Option fällt mit zurückgehender Volatilität aufgrund des Vegas.
Beispiel der Optionskennzahl Vega:
- 200er Put-Option,
- 101 Tage Restlaufzeit
- Optionspreis: $ 9,38
- Vega = 0,42
- Nimmt die Volatilität um 1 % ab, dann fällt der Optionspreis: $ 9,38 – 0,42 = $ 8,96
- Steigt die Volatilität um 1 % an, dann steigt der Optionspreis: $ 9,38 – 0,42 = $ 9,80
Das Theta einer Option
Das Theta beschreibt die Änderungsrate des Optionspreises pro Tag. In der Praxis ist damit der klassische Zeitwertverlust gemeint. Das Theta ist immer negativ, da Zeit nur vergehen und nicht zurückkommen kann. Bei At-The-Money-Optionen ist das Theta am größten.
Das Theta
Optionsgriechen werden immer aus Sicht des Optionskäufers betrachtet, daher müssen Käufer einer Option das Theta als Zeitwertverlust hinnehmen. Je näher die Restlaufzeit der Option zum Verfallstag rückt, desto größer ist das Theta.
Das Rho einer Option
Ändert sich der risikofreie Zins, hat dies Auswirkungen auf unsere Optionen. Welche genau wird mit dem Wert Rho angegeben. Der Wert ist bei Call-Optionen stets positiv, bei Put-Optionen hingegen immer negativ.
Da sich der risikofreie Zins eher selten verändert und wir ihn ohnehin nicht beeinflussen können, ist das Rho in der Praxis durchaus zu vernachlässigen. Dies wird sich auch in den kommenden Jahren kaum ändern, da wir in absehbarer Zeit keine Hochzins-Phasen erleben werden.
Fazit zu den Optionsgriechen
Die Optionsgriechen sind wichtige Kennzahlen für Optionshändler. Mit den Greeks lassen sich verschiedene Veränderungen einzelner Faktoren und dessen Einfluss auf den Optionspreis berechnen. Neben Delta, Gamma, Vega, Theta und dem Rho gibt es auch noch das Omega. Diese Sensitivitätskennzahl gibt an, wie viel Prozent sich der Optionspreis ändert, wenn sich der Basiswert um 1 Prozent ändert.
Mit den Griechen können Optionshändler abschätzen, wie sich die einzelnen Optionspreise bei bestimmten Veränderungen bewegen und so viele verschiedene Optionsstrategien aufsetzen.
Häufige Fragen zu den Optionsgriechen
Was sind die Optionsgriechen?
Die Optionsgriechen sind Kennzahlen mit denen Optionshändler die Entwicklung des Optionspreises in Abhängigkeit verschiedener Einflussfaktoren berechnen können.
Was ist das Delta einer Option?
Das Delta einer Option gibt die Änderungsrate des Optionspreises an, falls sich das Underlying um $ 1 erhöht.
Was ist das Gamma einer Option?
Das Gamma einer Option gibt die Änderungsrate des Deltas an, falls sich das Underlying um $ 1 erhöht.
Was ist das Vega einer Option?
Das Vega einer Option gibt die Änderungsrate des Optionspreises in Abhängigkeit der Volatilität an.
Was ist das Theta einer Option?
Das Theta einer Option gibt die Änderungsrate des Optionspreises pro Tag an.
Was ist das Rho einer Option?
Das Rho einer Option gibt die Änderungsrate in Abhängigkeit des risikolosen Zinses an.
Was ist das Omega einer Option?
Das Omega einer Option gibt an, um wie viel Prozent sich der Optionspreis ändert, wenn sich der Basiswert um 1 % ändert.
Hinweis:
Dieser Beitrag dient nur der Information und stellt keine Aufforderung zum Kauf oder Verkauf der erwähnten Wertpapiere dar. Der Handel mit börsennotierten Wertpapieren kann zum Teil erheblichen Kursschwankungen unterliegen, die zu erheblichen Verlusten bis hin zum Totalverlust führen können. Bei jeder Anlageentscheidung, die Sie aufgrund von Informationen, welche aus Inhalten dieser Seite hervorgehen, treffen, handeln Sie immer eigenverantwortlich, auf eigene Gefahr und eigenes Risiko. Die auf dieser Seite zur Verfügung gestellten Inhalte, wie z.B. Handelssignale und Analysen, beruhen auf sorgfältiger Recherche, welchen Quellen Dritter zugrunde liegen. Diese Quellen werden von dem Autor als vertrauenswürdig und zuverlässig erachtet. Der Autor übernimmt gleichwohl keinerlei Gewährleistung für die Aktualität, Richtigkeit oder Vollständigkeit der Inhalte und haftet nicht für materielle und/oder immaterielle Schäden, die durch die Nutzung oder Nichtnutzung der Inhalte oder durch die Nutzung fehlerhafter und unvollständiger Inhalte verursacht wurden.